关于最优停止问题的研究

摘要：本文就最优停止问题进行了研究，最优停止问题是博弈论中的一个经典问题，它可以具体描述为各种实际问题。本文采用理论分析与代码模拟的方式，从数学与计算机模拟两个角度来研究与解决这个问题，最终发现是该问题的解，也就是最优采样比率。同时还发现此时选取到最优值的概率也为。

一、介绍

在概率及博弈论上，最优停止问题是一系列问题的统称，它包括如捡稻草问题、恋爱问题、秘书问题等等。拿捡稻草问题举例，一片稻田上有n株稻草，每株稻草长度都不一样，你从稻田的这一头走到另一头，其中你捡一株稻草，但你不能回头，问如何尽可能地捡到最长的那根稻草。在这个问题中，我们的策略是先观察前k株稻草，但都不捡，记下前k株稻草中最长的那一株，之后观察后面的n-k株稻草，一旦遇到比前k株中最长的那一株要长的稻草就把这株稻草捡起来。最优停止问题所要求解的就是这个k与n的关系，也就是将多少株稻草作为样本空间去观察的问题。同样的策略求解也存在在于恋爱问题、秘书问题中。为了求解最优停止问题，我准备了数理的解决方式与代码模拟的解决方式，最终这两种方式得到了一致的结论。

二、数理分析

同样以稻草作为例子展开我们的数理分析。假设一共有株稻草，我们将株稻草作为样本空间进行观察。那么对于每一个，如果最长的稻草在第个位置(在到之间)，那么该稻草被选中当且仅当前株稻草中最长的那株稻草在前株稻草之中，其可能性为。所以我在下方给出放弃前个人，将这个人作为样本空间选到最优的人的概率。

那么这道题就变成了求当为何值时，得最大值，其中且属于正整数。当较小时，可以用非线性规划求整数解，但我们的最优停止问题，考虑的是很大的情况。当很大时，可以观察出是将区间分割成宽度为的小区间的黎曼和，令，易得。

为求最大值，令，则，同时得出一个附加的结论，此时。

综上所述，最优停止问题的解为 ,同时可以求出当为时选取到最大值的概率也为。

三、代码模拟

除了上面的数理分析，我还用代码模拟了最优停止问题，并输出了横坐标为观察的样本空间大小（也就是k值），纵坐标为得到最优解次数的图表。接下来我将讲解我的代码设计思路以及展示我的模拟结果。为了讲解更为生动形象，我同样以捡稻草作为例子。

首先假设一共有100株稻草，稻草长度都不一样，在代码中我通过一个容纳正整数1到100的数组来表示这些稻草，同时定义一个有100个元素的score数组来记录各个观察样本数量选取到的最长的稻草的次数。之后是模拟选择的过程，对于k值也就是观察样本的数量，我设置了从0到99。每一次先得出并记录前k个数的最大值，在剩下的数字中，一旦有大于这个最大值的数字就记录这个数字并跳出循环。每一次模拟选择稻草的过程前先将数组中元素的次序打乱，对于每一次选取的结果，如果选到最大值，则更新score数组中相应下标的元素值。为了让结果尽量可信，我将选取的总次数也就是外循环的值设置地很大，设置为了10000。最终，通过python的matplotlib包，我将模拟的结果可视化，横坐标为选取作为观察样本的数量，纵坐标为成功选到最大值的次数。经过多次运行，我发现峰值总是出现在36与37之间，同时可以观察到纵坐标的最大值约为3700，而3700/10000与1/e又十分接近，这两点都与我数理分析得到的结论相一致。（代码详见附录）

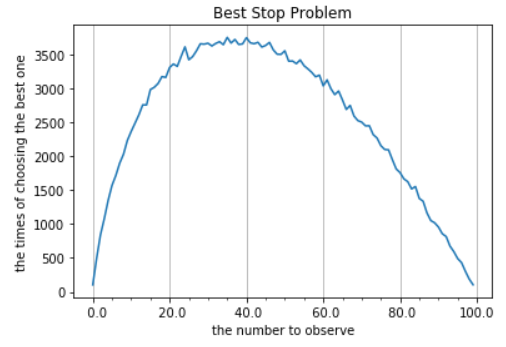
result-of-code

四、结论

通过这次的研究，我通过数学的逻辑推理和计算机的模拟成功地解出了最优停止问题的答案，作为一个非常实用的概率、博弈论结论，最优停止问题的答案告诉我们的结论不仅告诉我们在具体的选择场景中先观察 1� 的样本再去进行选择，而且很抽象哲学地告诉我们在做事情时要先去观察、思考这件事物，不要盲目行事也不要不敢迈出步子。

附录

import time
import random
import matplotlib.pyplot as plt
from matplotlib.ticker import MultipleLocator, FormatStrFormatter

random.seed(time.time())
chooseArray=[]
score=[]

for i in range(1,101):
    chooseArray.append(i)
for i in range(0,100):
    score.append(0)
for i in range(0,10000):
    for k in range(0,100):
         random.shuffle(chooseArray)
         max=0
         chooseFlag=False
         choose=0
         j=0
         while j<k:
            if(chooseArray[j]>max):
                max=chooseArray[j]
            j=j+1
         while j<100 and not chooseFlag:
            if(chooseArray[j]>max):
                chooseFlag=True
                choose=chooseArray[j]
            j=j+1
         if not chooseFlag:
            choose=chooseArray[99]
         if(choose==100):
            score[k]+=1

#结果可视化
ax = plt.subplot(111)
x=range(0,100)
y=score
plt.plot(x,y)

xmajorLocator = MultipleLocator(20)  
xmajorFormatter = FormatStrFormatter('%5.1f')
ax.xaxis.set_major_locator(xmajorLocator)
ax.xaxis.set_major_formatter(xmajorFormatter)
xminorLocator = MultipleLocator(5)
ax.xaxis.set_minor_locator(xminorLocator)
ax.xaxis.grid(True, which='major')
ax.set_title('Best Stop Problem')
ax.set_xlabel('the number to observe')
ax.set_ylabel('the times of choosing the best one')